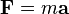Tercera ley de Newton o ley de acción y reacción
Concepto
La tercera ley de Newton
explica las fuerzas de acción y reacción. Estas fuerzas las ejercen todos los
cuerpos que están en contacto con otro, así un libro sobre la mesa ejerce una
fuerza de acción sobre la mesa y la mesa una fuerza de reacción sobre el libro.
Estas fuerzas son iguales pero contrarias; es decir tienen el mismo modulo y
sentido, pero son opuestas en dirección. Esto significa que siempre en que un
cuerpo ejerce una fuerza sobre otro este también ejerce una fuerza sobre él. Se
nombra fuerza de acción a la que es ejercida por el primer cuerpo que origina
una fuerza sobre otro, por lo tanto se denomina fuerza de reacción a la es
originada por el cuerpo que recibe y reacciona (De allí el nombre) con esta
otra fuerza sobre el primer cuerpo. ¿Pero qué pasa cuando ningún cuerpo origino
primariamente la fuerza, como en el ejemplo del libro sobre la mesa? Cualquiera
puede ser denominada fuerza de acción y obviamente a la otra se le denominará
como fuerza de reacción.
Ecuación
La ecuación que utilizamos para resolver ejercicios de acción y reacción es la de
F=m.a
F=m.a
Problema con la tercera ley de Newton
Consideramos un cuerpo
con un masa m = 2 Kg. que está en reposo sobre un plano horizontal, como el
indicado en la figura 17. a) Haz un diagrama de cuerpo libre. b) Calcular la
fuerza con que el plano reacciona contra el bloque.

Las fuerzas que actúan
sobre el bloque están representadas en la figura 18, donde se elije un eje de
coordenadas cuyo origen es el centro del cuerpo, mostrándose las fuerzas
verticales: el peso  y la normal
y la normal 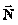 .
.
 y la normal
y la normal 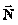 .
. El peso del cuerpo,
dirección vertical y sentido hacia abajo.
El peso del cuerpo,
dirección vertical y sentido hacia abajo.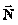 Normal, fuerza que el
plano ejerce sobre el bloque.
Normal, fuerza que el
plano ejerce sobre el bloque.
Al diagrama así mostrado
se le llama diagrama de cuerpo libre.
N – P = m . a
N – P = 0
N = P
N = m . g (porque P = m
( g)
N = 2 Kg . 9,8 m/s2
N = 19,6 N
Aplicaciones de la
tercera ley de Newton
La fuerza que ejerce la
bala sobre la pistola y la que ejerce la pistola sobre la bala provocando el
disparo de esta. La fuerza que ejerce el avión sobre el aire, provoca que el
aire reaccione sobre el avión provocando el desplazamiento de este. La fuerza
del misil hacia el aire y la del aire sobre el misil provoca el movimiento del
misil. La fuerza que la mano ejerce sobre la mesa y la que esta ejerce de
vuelta no da como resultado el movimiento debido a que las fuerzas son muy
leves como para provocarlo. La fuerza que ejerce el remo sobre el muelle no es
suficiente como para moverlo pero la fuerza de reacción del muelle si es
suficiente como para mover al remo hacia atrás, llevando al hombre hacia atrás,
por lo que el bote es arrastrado hacia atrás.
Simulador: