SEGUNDA LEY DE NEWTON O LEY DE LA FUERZA
Concepto
La aceleración de un
objeto es directamente proporcional a la fuerza neta que actúa sobre él e
inversamente proporcional a su masa.
Esta ley explica qué
ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser
constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento,
cambiando la velocidad en módulo o dirección. En concreto, los cambios
experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza
motriz y se desarrollan en la dirección de esta; las fuerzas son causas que
producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la
causa y el efecto, la fuerza y la aceleración están relacionadas. Dicho
sintéticamente, la fuerza se define simplemente en función del momento en que
se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma
tasa de cambio en el momento del objeto.

Ecuación
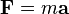
Problema con la segunda ley de Newton
Una fuerza le
proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la
magnitud de dicha fuerza en Newton.
Datos
m = 2,5 Kg.
a =1,2 m/s2.
F =?
Solución
Para calcular la fuerza
usamos la ecuación de la segunda ley de Newton:

Sustituyendo valores
tenemos:

Aplicaciones de la segunda ley de Newton
Las aplicaciones de la
segunda ley de Newton son innumerables y se pueden encontrar en multitud de
campos de estudio, tales como la medicina, la zoología, la geología, la física,
la química o la ingeniería.
En el ámbito de la
medicina y especialmente en traumatología,
la segunda ley de Newton puede llegar a ser muy útil para conocer las
fuerzas a las que sometemos a nuestros huesos. Por ejemplo, cuando recibimos un
golpe en un hueso, éste es sometido a una aceleración, que es consecuencia
directa de la fuerza del golpe. Si dicha fuerza supera un determinado valor, el
hueso podría fracturarse. En este caso, medimos la aceleración del hueso
durante el golpe y luego calculamos la fuerza que la provoca mediante la
segunda ley de Newton para ver lo cerca que hemos estado de la fractura.
Simulador:
No hay comentarios:
Publicar un comentario