ARTICULO #1
Operaciones con Vectores por el Método del
Paralelogramo
Para
utilizar métodos gráficos en la suma o resta de vectores, es necesario
representar las cantidades en una escala de medición manipulable. Es decir, podemos representar un vector
velocidad de 10 m/s hacia el norte con una flecha indicando hacia el eje y
positivo que mida 10 cm, en la cual, cada cm representa una unidad de magnitud
real para la cantidad (1 m/s).
El vector que resulta de operar dos o más vectores,
es conocido como el vector
resultante, o simplemente la resultante.
El método del paralelogramo permite sumar dos vectores de manera sencilla.
Consiste en colocar los dos vectores, con su magnitud a escala, dirección y
sentido originales, en el origen, de manera que los dos vectores inicien en el
mismo punto.
Los dos vectores forman dos lados adyacentes del paralelogramo. Los
otros lados se construyen trazando líneas paralelas a los vectores opuestos de
igual longitud.
El vector
suma resultante se representa a escala mediante un segmento
de recta dado por la diagonal del paralelogramo, partiendo del origen en el que
se unen los vectores hasta la intersección de las paralelas trazadas.
Ejemplo. Una bicicleta parte desde un taller de reparación y se
desplaza (4 m, 30º) y luego (3 m, 0º). Encuentre el desplazamiento total de la
bicicleta, indicando la dirección tomada desde el taller.
El desplazamiento total se da en dos tramos. Cada tramo desplazado se
representa por los vectores d1 y d2. El desplazamiento total es D = d1 y d2.
Los dos vectores son dibujados a la misma escala, y se colocan en el
mismo origen. Luego se trazan las líneas paralelas.
Si medimos con una regla, a la escala dada, el
tamaño del vector resultante debe dar aproximadamente 6.75 unidades de la
escala; es decir, la magnitud del vector desplazamiento total es de 6.75 m.
La medida de la dirección se toma con la ayuda de un transportador, y
debe dar aproximadamente 17º desde el origen propuesto.
El sentido del vector resultante es positivo, según el marco de
referencia común (plano cartesiano, hacia x positivo y hacia y positivo).
Entonces como resultado, la bicicleta se desplaza (6.75 m, 17º).
Operaciones con Vectores por el Método del Polígono
Éste es el método gráfico más
utilizado para realizar operaciones con vectores, debido a que se pueden sumar
o restar dos o más vectores a la vez.
El
método consiste en colocar en secuencia los vectores manteniendo su magnitud, a
escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del
anterior. El vector resultante está dado por el segmento de recta que une el
origen o la cola del
primer vector y la punta flecha del último vector.
Ejemplo. Sean los vectores:
Encontrar.
Resolviendo
por el método del polígono, la figura resultante es:
Si se utilizan los instrumentos de medición
prácticos, se obtiene que:
y que θ es aproximadamente 80ª.
Cuando dos vectores se restan, el
procedimiento anterior es el mismo, lo único que cambia es el sentido del vector que le sigue al signo menos. Por
ejemplo, al restar el vector D2 del vector D1 se tiene:
D1- D2
= D1+ (-D2).
La
expresión del miembro derecho de la ecuación anterior designa un cambio en el
sentido del vector D2; entonces, la expresión queda como una suma, y por lo
tanto, se sigue el procedimiento del método gráfico mostrado anteriormente.
Los
métodos gráficos ofrecen una manera sencilla de sumar o restar dos o más
vectores; pero cuando las magnitudes de los vectores son demasiado grandes o
poseen una gran cantidad de decimales, éstos métodos se vuelven imprecisos y
difíciles de manipular a escalas de medición menores.
Es por
eso, la necesidad de un método matemático nemotécnico, que permita dar una
mayor precisión en el cálculo de vectores resultantes, no sólo en la magnitud,
sino además en la dirección de ellas.
En la siguiente lección se muestra éste
método, que sugiere el estudio previo de las funciones trigonométricas, debido a que se basa en la trigonometría de un triángulo
rectángulo.
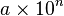
, un número real mayor o igual que 1 y
menor que 10, que recibe el nombre de coeficiente.
, un número entero, que recibe el
nombre de exponente u orden de magnitud.
